In issue number 393 of his popular newsletter The Embedded Muse, Jack Ganssle took a look at the performance of trig functions. Trigonometric functions such as cos are often used in time critical calculations. In particular, he compared the C math library against a custom implementation. I think this kind of analysis is essential for solid embedded engineering and therefore I really enjoyed the article.

Today, I will try to reproduce his results using our microbenchmark platform.
barebench.com is a tool which allows you to quickly measure the runtime of functions on embedded targets. The measurements are automatically executed on the real microcontroller hardware. You do not need any lab setup or hardware to use barebench.

As we will see, it is important to measure your implementation because there are several pitfalls you may run into when doing floating point calculations.

We will use a Cortex M4F for our measurements. The core clock is running at 16 MHz with 0 flash wait states. This is similiar to Jacks setup and differs only in the core clock. Since we will normalize all results to clock cycles, this should have no influence on the results.

Our examiniation will be limited to the the cos function from the C math library and his custom cos_32 function (a cosine approximation accurate to 3.2 decimal digits). To allow for easy comparision, I normalized his results for these 2 functions to clock cycles:

Function	Provenance	Argument precision	Min (Cycles)	Max (Cycles)	Mean (Cycles)
cos	C Math Lib	Single	96	154	146
cos_32	Custom Approximation	Single	20	21	20

The first comparison

We start by taking the published source code and compare it against the C math library cos function. As inputs, we will use decimal degrees from 50° to 360° and convert them to radiant.

In case you want to play with the benchmarks on your own, you can load the barebench sample project TrigFunctionExamination. Make sure you log in before opening the link.

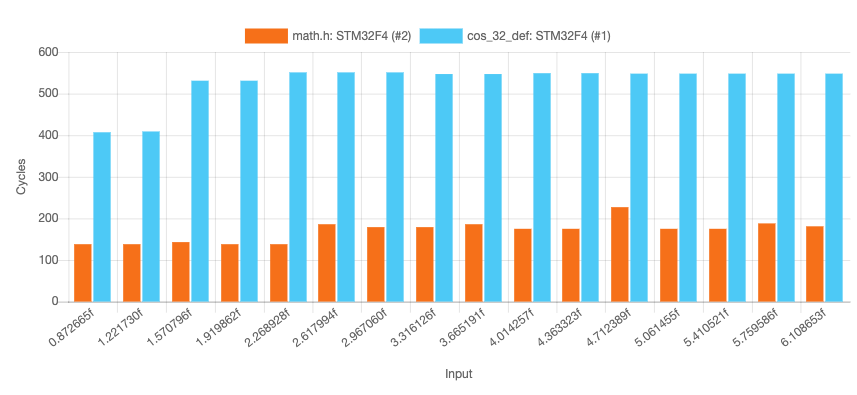
The results are surprising. The custom implementation seems to be way slower. We will dig into this in a moment, but first let’s compare these numbers to the ones determined by Jack Ganssle (his results in braces):

Function	Provenance	Argument precision	Min (Cycles)	Max (Cycles)	Mean (Cycles)
cos	C Math Lib	Single	138 (96)	227 (154)	170 (146)
cos_32	Custom Approximation	Single	407 (20)	551 (21)	528 (20)

The results for the C Math Lib are comparable. The little difference there is might be explained by

• Different input data. As you see from the results, the runtime depends slightly on the given input.
• Different compilers. Jack is using the mbed compiler, which is based on ARMCC / clang. We use the open source arm gcc. However the standard library function is very likely highly optimized in both cases.
• The way the measurements are done. barebench uses the DWT Core Clock Counter and is therefore precise down to the clock cycle and does not incur any runtime overhead due to pin toggling or other more conventional methods of benchmarking.

Explaining the bad performance of cos_32

Now, we can turn our attention to the huge difference for the cos_32 function. The runtime I observed is more than 25 times longer than Jack’s data suggested. Enabling assembly output, we see that there are several branches to functions like __aeabi_f2d.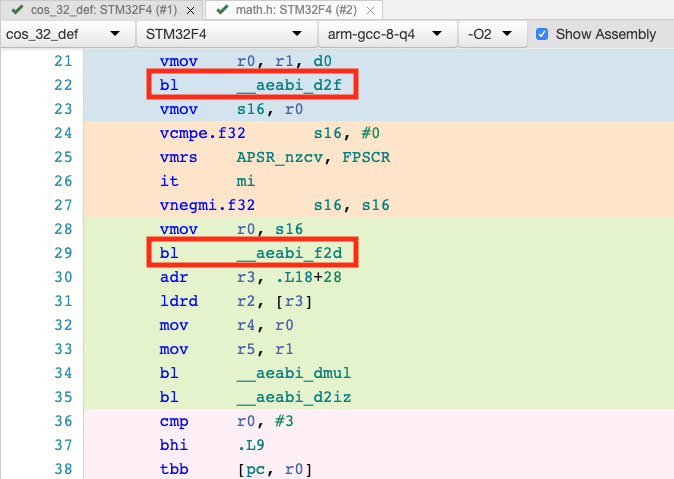

These functions convert between single precision and double precision floating point values. The Cortex M4 floating point unit (FPU) only supports single precision. This means all operations requiring double precision are usually done in software and therefore at least an order of magnitude slower than the corresponding hardware operation.

Removing double constants

If you take a look into the cos_32 implementation you will see, that a whole range of global constants are declared as double. I changed these types to float and also removed all unnecessary functions for the sake of readability. You can take a look at this code in the cos_32_float tab in the TrigFunctionExamination sample project.

Benchmarking these two versions of cos_32 against each other yields the following result:

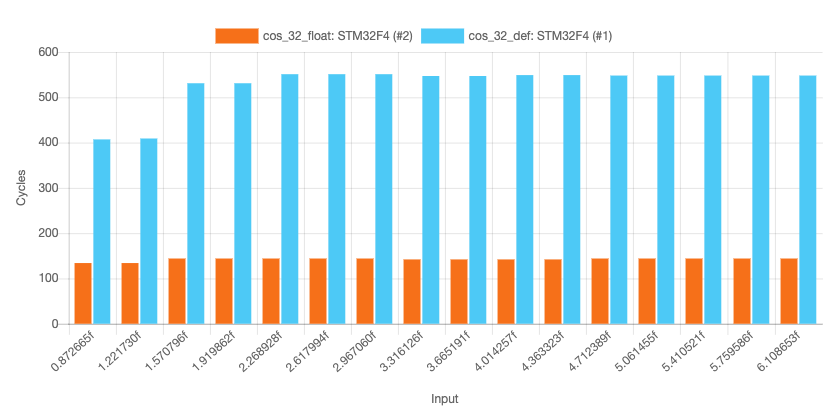
A few observations:

• Using the table result view from barebench, we see that the return values between both functions exactly match. Changing the constants from double to float therefore has no implication on accuracy!
• The runtime is almost independent of its input data (min: 134, max: 144, mean: 142 clock cycles). That kind of determinism is always a plus in embedded.
• The results are unfortunately still far away from the mean of 20 cycles in Jacks results.

Looking at the assembly of cos_32_float, you will notice that it consists in large part of instructions prefixed with a “v” (vldr, vcmpe, vmul, vcvt, …). These are the ARM floating point instructions. This kind of ouptut is desired, when the FPU is supposed to shoulder much of the calculation.

Removing range reduction

However, there is still one branch to a software library function (fmod), which might be slow and responsible for our poor performance. If you look at our cos_32 code, you will discover that this function is called on purpose:

float cos_32(float x){
    int quad;                          // what quadrant are we in?
    x=fmod(x, twopi);                  // Get rid of values > 2* pi
    if(x<0)x=-x;                       // cos(-x) = cos(x)
    quad=int(x * two_over_pi);         // Get quadrant # (0 to 3) we're in
    switch (quad){
        case 0: return  cos_32s(x);
        case 1: return -cos_32s(pi-x);
        case 2: return -cos_32s(x-pi);
        case 3: return  cos_32s(twopi-x);
    }
}

fmod is used for a process called range-reduction. We know that we are only using input values between 0 and 360° however, so we can omit this reduction. In our barebench example, this version is called cos_32_float_no_range_red. I benchmarked this version as well and added it as a new row to our comparison.

Function	Provenance	Argument precision	Min (Cycles)	Max (Cycles)	Mean (Cycles)
cos	C Math Lib	Single	138 (96)	227 (154)	170 (146)
cos_32	Custom Approximation	Single	407 (20)	551 (21)	528 (20)
cos_32_float_no_range_red	Custom Approximation	Single	32	42	41

The huge discrepancy between my results and the ones in Jacks original post disappeared. However, there is still a factor of 2 between them. It would be interesting to see if this is due to a) benchmarking differences or b) more efficient code generated the ARM CC compiler.

Takeaways

• Always make sure that you are not accidentally using software emulation, for example by employing double instead of float data types.
• Interface constraints (such as limiting the input range to 0..360°) can have huge runtime implications.
• After several changes, we were able to match Jack Ganssles results closely.

You can reproduce all the results by yourself with the barebench sample project TrigFunctionExamination. Make sure you log in before opening the link.

If you are interested in doing runtime measurements for your custom toolchain and microcontrollers, check out the ExecutionPlatform. It is a development tool that makes target-dependent jobs much easier. barebench is based on it.